技術コラム Column
- si
- 連載コラム :シグナルインテグリティ(SI)改善のポイント
クロストークのモデルと発生メカニズム
シグナルインテグリティ改善のポイント第 5~6 回でクロストークに関して解説してきましたが、今回(第7回)も引き続きクロストークについて、モデル化の方法や発生メカニズムについて解説し、次回(第 8 回)はクロストークのピーク電圧の算出方法を紹介し、シミュレーションとの整合性の検証を行っていきたいと思います。 また、マイクロストリップ線路とストリップ線路でのクロストークの違いについても見ていこうと思います。
目次
重ね合わせの理
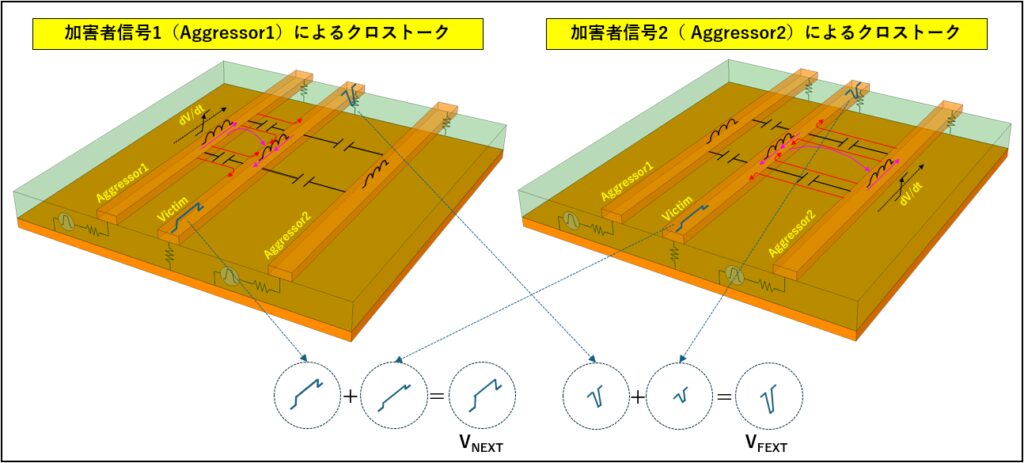
一般的に線形受動システムでは、重ね合わせの理が成立するため、同一ネット上にある複数の信号を互いに独立して計算し、加算することで、そのネット上に現れる波形を求めることが出来ます。 クロストークを解析するには、この重ね合わせの理が役立ちます。ある被害者信号に現れるクロストークノイズは、この被害者線路と結合している複数の加害者線路からの結合により発生するそれぞれのクロストークノイズの和となります。 これをイメージしたものを図 1 に記します。
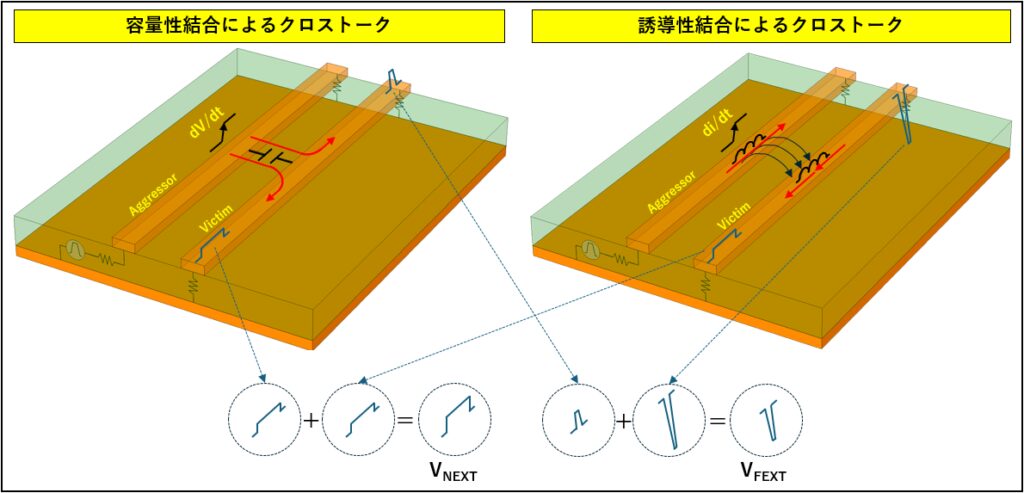
また、クロストークには容量性結合によるものと誘導性結合によるものが存在します。 これらを別々に算出し、それぞれ足し合わせることでトータル的なクロストーク量を算出することも出来ます。 これをイメージしたものを図 2 に記します。
クロストークモデル
プリント基板上の伝送線路は、回路図上では単なる接続線ですが、クロストークを解析するためには、伝送線路に含まれる寄生成分を考慮しなければなりません。 クロストークを解析する最適な方法は、結合伝送線路の形状を、電磁界解析ソフトを利用してSパラメータでモデル化し、終端抵抗を加えて、時間ドメインや周波数ドメインで解析することです。 また、等価回路モデルを使用することでも、結合伝送線路の形状と終端を考慮した解析が可能になります。 例えば平行する2本の結合伝送線路の無損失でのモデル化であれば、図 3 のようなL,C 寄生成分を含めた等価回路モデルを使用して解析します。

この図で、Lmを相互インダクタンス、Cmを相互キャパシタンスと呼び、これらが線路間の結合を生み出すことで、クロストークノイズが発生することになります。
伝送線路の場合は、ここに現れるLやCは、分布定数として考えなければならないのですが、SPICE系シミュレータの場合、分布定数を取り扱うことが出来ません。 そのため、伝送線路を複数のセクションに分割し、1セクションの線路長に応じた定数を割り当てた集中定数回路に変換して近似計算を行うことになります。 SPICE によっては、伝送線路を含めた解析に対応している場合もありますが、結局、内部的には伝送線路を複数のセクションに分割して計算をしているものと思われます。
複数のセクションに分割した集中定数回路モデルで解析する場合、分割する数に注意が必要です。 必要な分割数 n は、必要となる帯域幅と伝搬遅延時間によって以下の式で求めることが出来ます。

2種類ある容量マトリクス
フィールドソルバを使用することで、伝送線路に存在する寄生成分を行列にした容量マトリクスとインダクタンスマトリクスを簡単かつ十分な精度で求めることが出来ます。 注意しなければならないのは、容量マトリクスには、マクスウェル容量マトリクスとSPICE容量マトリクスの2種類が存在しているということです。 そして、SPICE系シミュレータを使用するためには、SPICE容量マトリクスを使用する必要があります。 フィールドソルバから出力される容量マトリクスはマクスウェル容量マトリクスで出力されている場合が多く、この場合は、SPICE容量マトリクスに変換する必要があります。 SPICE容量マトリクスの対角要素は単に該当する導体とGND間の容量を表しているのに対し、マクスウェル容量マトリクスの対角要素はその導体の全負荷容量を表し、非対角要素は、便宜上、負の値を取っています。
マクスウェル容量マトリクスから、SPICE容量マトリクスへの変換は、以下のように行います。
マクスウェル容量マトリクスからSPICE容量マトリクスへの変換例を以下に示します。

ここで表されるキャパシタンスとインダクタンスは単位長当たりの値なので、単位は、“F”や“H”ではなく、“F/m”や“H/m”などの分布定数になります。 繰り返しになりますが、SPICEシミュレータなどで複数セクションに分割した集中定数回路として解析する場合は、線路長と分割数に応じて数値を変更する必要があります。
容量性結合によるクロストーク
ここから、クロストークが発生するメカニズムについて、容量性結合と誘導性結合に分けて解説してみようと思います。
図6は、容量性結合によるクロストークで発生する被害者線路の電流を図示したものです。 信号源が加害者線路を駆動し、信号源にエッジが生じると、このエッジ(図の場合、立上りエッジ)は、伝送線路の伝搬速度で、信号源から負荷端に向かって進んでいきます。 この時、容量性結合により被害者線路に電圧変動(dV/dt)が発生している部分だけに変位電流が流れます。 図6では、エッジが伝送線路の中間付近を通った瞬間に流れる変位電流を表しています。 この瞬間は伝送線路の他の部分で変位電流は流れません。
被害者線路の特性インピーダンスが均一であるため、加害者線路から被害者線路に流れた電流は、半分に分けられ、近端・遠端の両方向に向かって進むことになります。
図7はエッジが信号源から負荷端まで移動する期間全体でのクロストークによる電流の動きを表したものです。
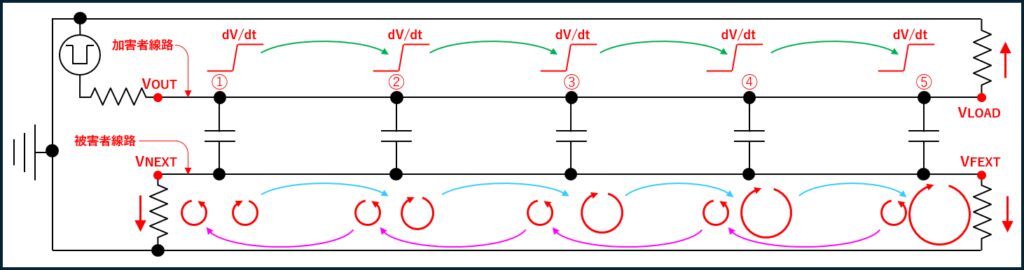
近端側に向かって流れる電流(図のピンク色矢印)は、図の①で発生したクロストークノイズ、②で発生したクロストークノイズ、③で発生したクロストークノイズ、、、と、バケツリレー式に近端にある終端抵抗に辿り着くため、一定の電流が終端抵抗に流れ続けます。 (ここでは離散的に表現していますが、実際にはこれが連続的に発生します。) このため、近端クロストーク電圧は結合配線長に関わらず一定の電圧※1になります。 この電流の流れは、遠端(図では⑤)で発生したクロストークが近端に戻ってくるまで続くので、図8のように、伝搬遅延時間の2倍のパルス長になります。
これに対し、遠端方向に向かって流れる電流(図の水色矢印)は、伝搬方向も伝搬速度も、加害者信号のそれ(図の緑色矢印)と等しいため、容量性結合によるノイズが連続的に追加され、雪だるま式に増加し続けます。 (例えば②の位置で考えると、①から②に進んだ電流に②のクロストークで発生した電流が加算される。) このため、配線長が長ければ長いほど遠端にある終端抵抗に流れる電流は大きくなります。 また、遠端クロストーク電圧は、配線長に加え、信号の立上り(立下り)時間が急峻であるほど大きく、短いパルスとなります。
図からもわかるように、近端クロストークは信号源のエッジと同時に、遠端クロストークは信号源からのエッジが負荷端に到達した時に、それぞれ現れることになります。 (図8参照)
※1伝送線路が臨界長よりも短い場合、電圧のピークは、より小さい値になります。
誘導性結合によるクロストーク
容量性結合同様、加害者線路から被害者線路に流れた電流は、半分に分けられ、近端・遠端の両方向に向かって進むことになります。 但し誘導性結合の場合、遠端に向かう電流の極性が逆極性(図の青色矢印)であることに注意して下さい。
図9は、誘導性結合によるクロストークで発生する被害者線路の電流を図示したものです。 信号源が加害者線路を駆動し、信号源にエッジが生じると、このエッジ(図の場合、立上りエッジ)は、伝送線路の伝搬速度で、信号源から負荷端に向かって進んでいきます。 この時、誘導性結合により被害者線路に電流変動(dI/dt)が発生している部分だけに誘導電流が流れます。 図9では、エッジが伝送線路の中間付近を通った瞬間に流れる誘導電流を表しています。 この瞬間は伝送線路の他の部分で誘導電流は流れません。

図10はエッジが信号源から負荷端まで移動する期間全体でのクロストークによる電流の動きを表したものです。
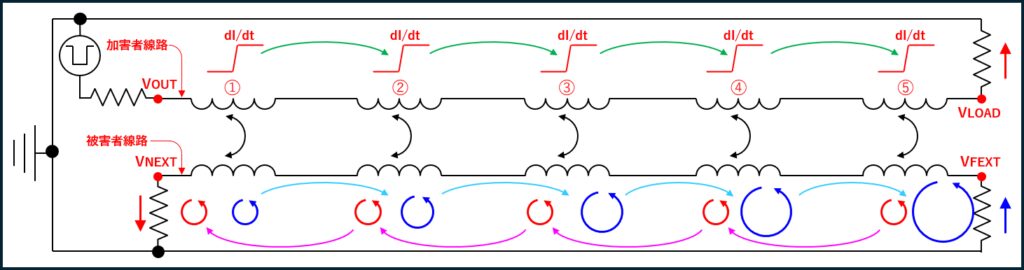
誘導性結合による近端クロストークも容量性結合の場合と同じような動作をします。 近端側に向かって流れる電流(図のピンク色矢印)は、図の①で発生したクロストークノイズ、②で発生したクロストークノイズ、③で発生したクロストークノイズ、、、と、バケツリレー式に近端にある終端抵抗に辿り着くため、一定の電流が終端抵抗に流れ続けます。 (ここでは離散的に表現していますが、実際にはこれが連続的に発生します。) そのため、近端クロストーク電圧は配線長に関わらず一定の電圧※2になります。 この電流の流れは、遠端(図では⑤)で発生したクロストークが近端に戻ってくるまで続くので、図11のように、伝搬遅延時間の2倍のパルス長になります。
これに対し、遠端方向に向かって流れる電流(図の水色矢印)は、伝搬方向も伝搬速度も、加害者信号のそれ(図の緑色矢印)と等しいため、誘導性結合によるノイズが連続的に追加され、雪だるま式に増加し続けます。 (例えば②の位置で考えると、①から②に進んだ電流に②のクロストークで発生した電流が加算される。) このため、結合配線長が長ければ長いほど遠端にある終端抵抗に流れる電流は大きくなります。 誘導性結合の場合、電流が終端抵抗を逆向きに流れるため、発生する電圧が逆極性となることに注意して下さい。 また、遠端クロストーク電圧は、配線長に加え、信号の立上り(立下り)時間が急峻であるほど大きく、短いパルスとなります。
図からもわかるように、近端クロストークは信号源のエッジと同時に、遠端クロストークは信号源からのエッジが負荷端に到達した時に、それぞれ現れることになります。 (図11参照)
※2伝送線路が臨界長よりも短い場合、電圧のピークは、より小さい値になります。