技術コラム Column
- pi
- 連載コラム :パワーインテグリティ(PI)改善のポイント
ターゲットインピーダンスの設定
本連載の第4回では、ターゲットインピーダンスに焦点を当てて解説していきたいと思います。
PDN上には、VRM、バルクコンデンサ、バイパスコンデンサ、EMIフィルタ、ICなど、多くの容量性・誘導性部品が存在し、更には、パターン、パッド、ビアなどのプリント基板コンポーネントにも寄生のキャパシタンスやインダクタンス成分が含まれています。 これらは相互に影響し合い、反共振によるインピーダンスピークを引き起こすことで、パワーインテグリティの問題を複雑にします。 また、近年使用されるプリント基板の殆どは多層構造であり、電源・GND専用層のプレーンの形状に伴う共振にも注意を払う必要があります。 電源・GND層に漏洩した高周波電流は、電源・GND層のプレーン形状に依存する周波数で共振し、EMI問題を引き起こします。
PI設計の最終目標は、PDN上に配置されたIC(アクティブ部品)が電源・GND端子から最大過渡電流を引き込んだ際に生じる電源電圧変動を、メーカが規定する許容範囲内に抑えることです。 そのためには、PDNのターゲットインピーダンスを規定し、PDNのインプットインピーダンスをターゲットインピーダンス未満に保たなければなりません。 インプットインピーダンスは周波数の関数であり、ICの過渡電流が含んでいる周波数全域で、その値がターゲットインピーダンス未満であることを確認しなければなりません。
目次
- ターゲットインピーダンスをメーカが規定している場合
- ターゲットインピーダンスのメーカ規定が無い場合
- Coffee Break : フーリエ変換について
- ターゲットインピーダンスと電源電圧変動の関係
- 二等辺三角波電流波形と高周波スペクトラム
- 最後に
ターゲットインピーダンスをメーカが規定している場合
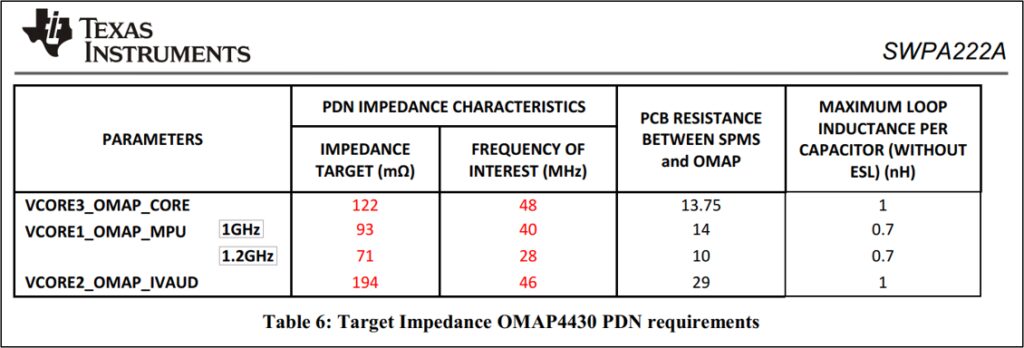
ターゲットインピーダンスは半導体メーカのデータシートやアプリケーションノートに記載されている場合があります。 例えば、図1はTexas Instruments社様のプロセッサ “OMAP4430”のApplication Reportの抜粋で、電源レールごとにターゲットインピーダンスとその最大周波数についての要件が規定されています。 こういった場合は、メーカが規定する要件を満たせば良いことになります。 最近では半導体メーカでターゲットインピーダンスを規定している例が増えてはきましたが、まだ規定されていない例も多く見受けられます。 そういった場合に、どのように見積もればよいのか、次の節以降で解説していきたいと思います。
ターゲットインピーダンスのメーカ規定が無い場合
ターゲットインピーダンスは、ICが最大過渡電流を引き込んだ時に、電源~GND端子間において、電源電圧変動がICの規定値内に収まることを保証するものですから、オームの法則から次のように定義することができます。 (過渡電流・インピーダンスは、周波数の関数になるので、 (f) を付けています。)

但し、最大過渡電流については、ICのデータシートに記載されていないことがほとんどです。 こういった場合、経験則として消費電流の半分を最大過渡電流として設定します。(エリック・ボガティン著 『高速デジタル信号の伝送技術』 より) 従って、ターゲットインピーダンスは、以下となります。
更に満たすべきターゲットインピーダンスの最大周波数についても考えなければなりません。 これは非常に悩ましい問題であり、使用するICごとに大きく異なり、必要な情報を入手することも困難です。
有限の立上り時間を持つパルス波の周波数スペクトラムは、高調波になるほど振幅が低下することがわかっています。 例えば、過渡電流はよく二等辺三角波として近似されますが、二等辺三角波の電流振幅はニー周波数を超えると40dB/decadeで低下します(図2)。 また、台形波の電流振幅は、第1ニー周波数を超えると20dB/decade、更に第2ニー周波数を超えると40dB/decadeで低下します(図3)。
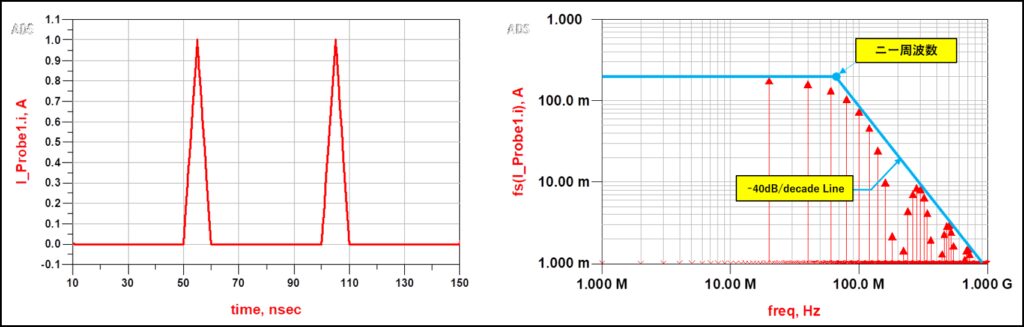
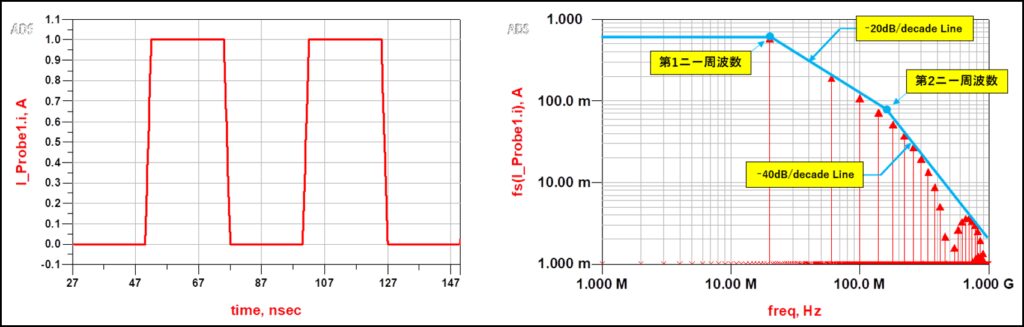
これらの事実から、ターゲットインピーダンスは、電流振幅が低下し始めるニー周波数から、オームの法則に基づいて20dB/decadeで増加させても良いことになります。 通常、PDNインピーダンスは高周波帯域で誘導性を示し、20dB/decadeで上昇しますが、ニー周波数より高い周波数帯では共振点が存在しない限り、この電流振幅の減少と相殺出来ると考えられます。
ニー周波数は、過渡電流の立上り時間が速いほど高くなりますが、最大過渡電流の立上り時間は、駆動する負荷に加え、IC内部のスイッチングゲートの最大数をどれだけ速くONできるかに依存します。 これらはチップのアーキテクチャ、パイプラインの数、マイクロコードなどによって異なり、クロックエッジの立上り時間~100 クロックサイクル程度までと大きな差があります。
Coffee Break : フーリエ変換について
フーリエ変換は、様々な波形を正弦波の和に分解して表現するためのツールです。 逆フーリエ変換により、分解された周波数成分から元の信号波形を復元することも可能です。
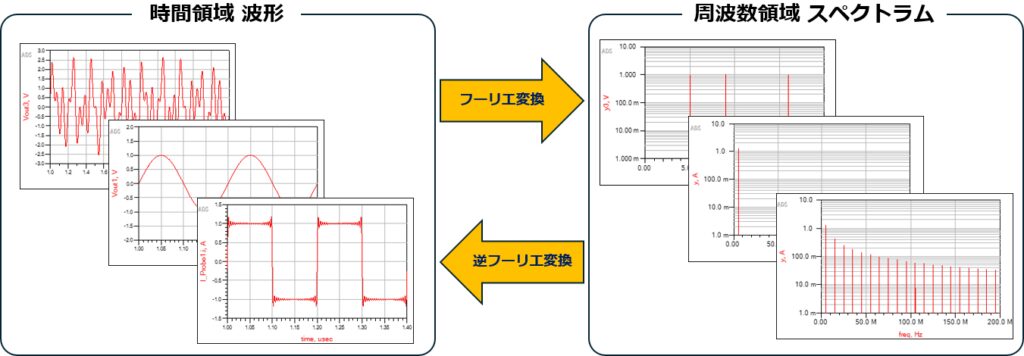
PDNに接続されるプロセッサやASICなどの負荷は、非常に高速で電流を変動させます。 この過渡電流に対して、PDNがどのような電圧変動を引き起こすかは、PDNのインピーダンス特性と過渡電流の各周波数成分の大きさに依存します。 このため、パワーインテグリティの評価は周波数領域を利用して行うのが一般的です。
重要なのは、時間領域波形と周波数領域スペクトラムは、同じ物理現象を異なる視点から表現したものであるということ、また、フーリエ変換(逆フーリエ変換)という数学的手法により、それらの間を行き来して分析することが可能であるということです。
ターゲットインピーダンスと電源電圧変動の関係
PDNのインピーダンスがICの電源~GND端子間の電圧にどのような変化を生じさせるのか、キーサイト社のAdvanced Design Systemを使用してトランジェント解析してみます。 図4はこの解析の模式図です。 Vcc:1V の定電圧源が、PDN 経由で負荷の IC に接続されます。 PDNには、PDN1とPDN2という2種類のインピーダンス特性を持つものを準備します。 図5の左側がPDN1、右側がPDN2をICから見たインプットインピーダンス特性を表しており、それぞれ、パスコンの配置が良好なものと、パスコンの配置が悪く、4.1MHz付近でインピーダンスピークが発生しているものとなっています。
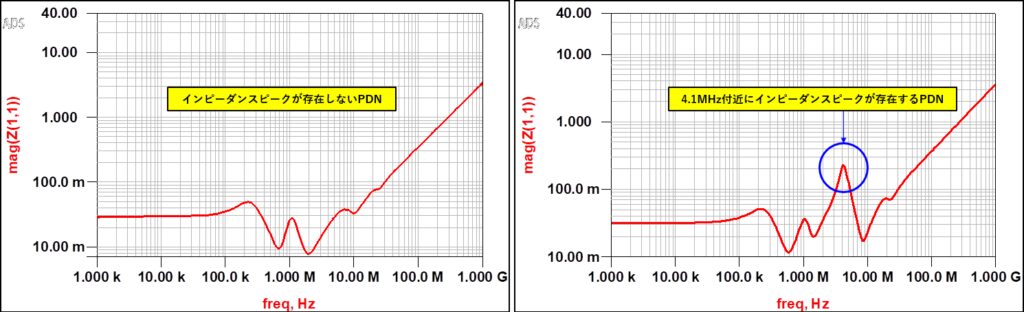
(右)PDN2:4.1MHz付近でインピーダンスピークが存在する。
VRM の負荷となるICは、電源端子から図6(左)のような立上り時間100ns、ピーク電流1A、周期500nsの二等辺三角波の過渡電流を引き込みます。 この過渡電流波形の周波数スペクトラムを図6(右)に示します。
ここで二等辺三角波のニー周波数は以下のように求まります。
このニー周波数を境にして、図7のように、ターゲットインピーダンスが一定値となる領域 [Region1 (fMin < f ≦ fKnee)] と、ターゲットインピーダンスを 20dB/decade で上昇させてもよい領域 [Region2 (fKnee< f< fMax)] とに分けられます。
許容電源電圧範囲を電源電圧 (1V) の 5% 、すなわち 1V±50mV とすると、 Region1、Region2 でのターゲットインピーダンスは、以下のようになります。
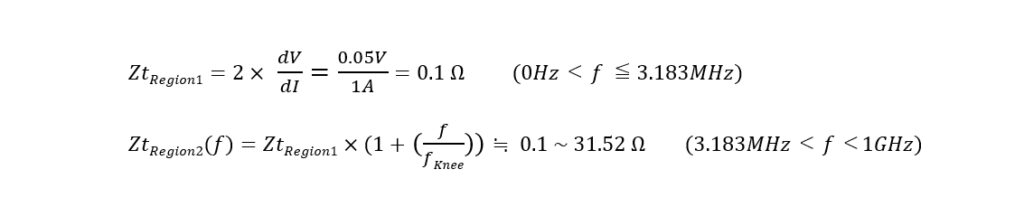
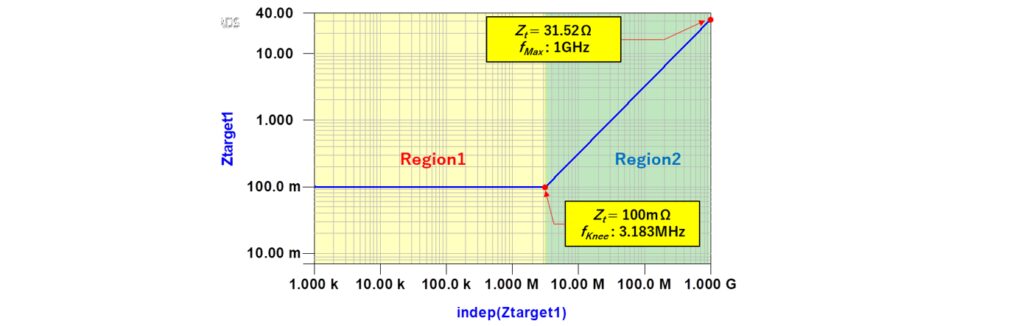
図5の2つのインプットインピーダンスと図7のターゲットインピーダンスを重ねて表示すると、図8のようになります。 PDN1はインプットインピーダンスの特性(赤色実践ライン)がターゲットインピーダンス(青色点線ライン)を完全に満たしていますが、PDN2は4.1MHz付近でターゲットインピーダンスを超えています。
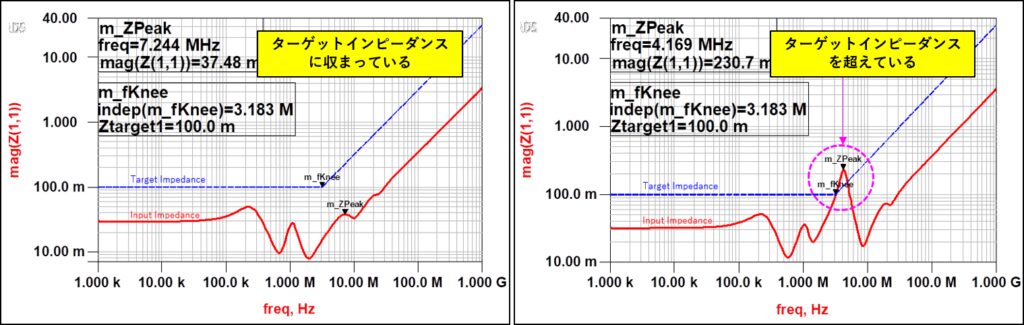
(右)PDN2:4.1MHz付近でターゲットインピーダンスを超えている。
PDN1およびPDN2を使用したこれらの構成でトランジェント解析を行い、ICの電源端子の波形を観測した結果を図9に示します。 PDN1を使用した場合、電源端子の波形はICの許容値内に収まっていますが、PDN2を使用すると許容値を超えていることが確認できます。 また、PDN2を使用した際に現れる大きな振幅の周波数を確認したところ、約 4.1MHz であり、これは図8のインピーダンスピークの周波数と一致しています。 このことから、大きな振幅の原因は、インプットインピーダンスの4.1MHz付近に現れるインピーダンスピークによるものと結論付けることができます。
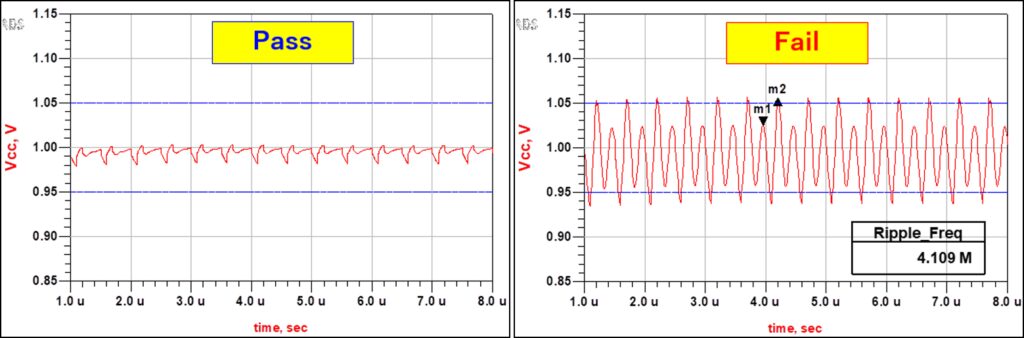
(右)PDN2を使用した場合のトランジェント解析結果
この解析例のように、インプットインピーダンスがターゲットインピーダンスを超える部分があると、ICの電源端子部での電圧変動が、メーカが規定する許容範囲を超えてしまう可能性があります。 インプットインピーダンスを解析し、ターゲットインピーダンスを超えないように PDN を設計することが、PDN の品質確保に繋がるということがご理解頂けるのではないでしょうか。
また、ターゲットインピーダンスを設定する上で、IC が引き込む最大過渡電流波形が重要です。 この後、この過渡電流波形についてもう少し堀り下げていこうと思います。
二等辺三角波電流波形と高周波スペクトラム
図10は、4つの立上り時間が異なる二等辺三角波の電流波形を表しています。(ピーク電流:1A、立上り時間:2.5ns , 5.0ns , 10.0ns , 15.0ns の4種類、周期:50ns)
これらの二等辺三角波を周波数スペクトラムで表すと、図11のようになります。 これらの波形の共通点は、基本波(1次高調波)における電流値が最も大きく、そこからニー周波数までは徐々に小さくなり、ニー周波数を超えた後は 40dB/decade の傾斜で減少している点です。
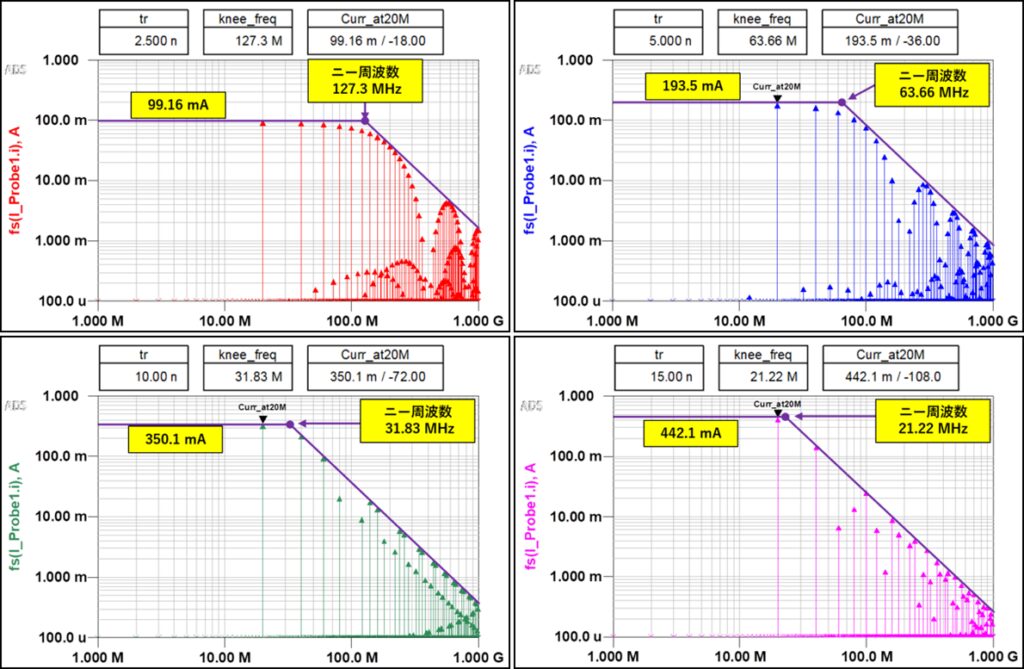
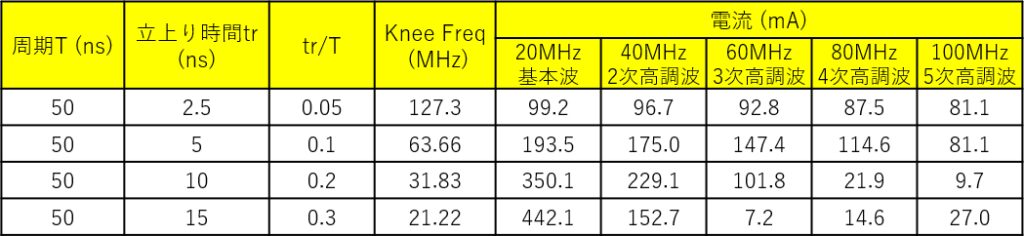
表1は、これら4つの電流波形のニー周波数と5次高調波までの電流値をまとめたもので、表2は、表1の「電流」の部分を「ピーク電流に対する割合」で表したものです。 二等辺三角波のピーク電流値(この場合は 1A)と、基本波(この場合20MHz)における電流値との割合(表の赤枠部分)は、信号の立上り時間と周期の比 (tr/T) により一定の値を取ります。 例えば、周期 50ns・立上り時間 5ns と、周期 10ns・立上り時間 1ns は、共に19% となります。
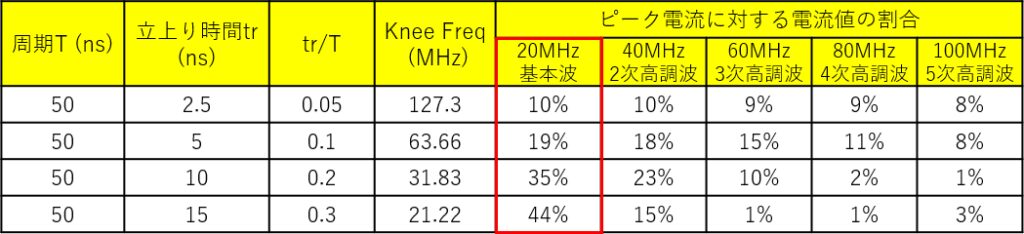
表を見ると、信号の立上り時間と周期の比 (tr/T)が大きくなると、この割合が大きくなっていくように見えますが、更に大きくしていくと、tr/T=0.38の時に46.1%で最大となり、これを境に減少に転じ、完全な三角波となる tr/T=0.5 では、40.5%まで下がっています。
これらのことから、二等辺三角波では、全周波数帯においてピーク電流の 50% を超える高調波スペクトラムは存在しないと結論付けることができます。
最後に
今回のコラムでは、ターゲットインピーダンスの考え方について言及してきました。 メーカ規定値が存在しない場合のターゲットインピーダンスの見積り方法についても触れました。 また、過渡電流を理想的な二等辺三角波とみなし、電流波形のスペクトラムについて解析を行いました。 実際の過渡電流が、どのような波形となりどのような周波数成分を含んでいるかは使用するデバイスに依存するため不明な部分も多いかと思いますが、ターゲットインピーダンスに関する考え方ついてはご理解いただけたのではないかと思っています。